从地球化学背景中分离并识别地球化学异常是地球化学勘探的主要任务之一。在过去的几十年中，地球化学异常已被很多方法识别^[1]。最早出现的是基于一元正态分布理论的方法，包括均值±2倍标准差、直方图、分位数-分位数图、盒图、概率图、单变量分析等^[2]。多元统计分析方法，如因子分析、主成分分析等，能够将地球化学数据减少到几个组分，从某种意义上，实现了降维，利用降维后的组分应用于地球化学异常识别，取得了较好的效果，曾经一度占据化探异常识别方法的主流^[3]。此外，空间统计方法，如移动平均技术、空间因素分析^[4]被用于识别多元地球化学异常，除浓度值频率分布外，还考虑了相邻样本之间的空间相关性和变化。多变量的方法通常要求地球化学数据符合已知的统计分布，如多变量正态分布，然而各种地质事件和复杂的地质过程通常会导致多变量的地球化学数据具有复杂的空间和频率特性^[5-6]，意味着地球化学数据的分布可能是未知的，因此大多数需要假设多元正态分布的普通多元统计技术受到限制^[7]。

近年来，处理地球化学资料和鉴定地球化学异常的研究已经取得了重要进展，分形/多重分形模型、成分数据分析和机器学习技术是地球化学数据处理领域中广泛关注与研究的热点^[8]。分形、多重分形模型于1994年首次由成秋明等提出^[9]。该模型考虑地球化学模式的频率和空间方差，是有效的地球化学异常识别方法。其中，浓度面积（C-A）模型已经成为分析勘探地球化学数据的基本工具^[10]，在此基础上，发展了频谱面积模型（S-A）^[11]、奇异性分析（LSA）^[12]等模型。由成分数据的闭合特性引发的伪相关问题，为地球化学异常分析带来了挑战。Aitchison等^[13]提出加法对数比变换（alr）、中心对数比变换（clr），Egozcue等^[14]提出等距对数比变换（ilr）来消除成分数据的闭合性。大数据和人工智能的兴起改变了人们处理问题的方式，从数据中学习地球化学规律^[15-17]。对于复杂未知的地球化学分布问题，机器学习因其具有的模拟复杂及非线性系统的能力，被看作是具有远大前景的方法^{[8, 18]}。Chen等^[19]应用单一类别支持向量机识别青海省兰陵早火地区多变量地球化学河流沉积物调查资料异常。Beucher等^[20]将ANN用于芬兰西南部的Sirppujoki河流域的土壤测绘。Chen等^[21]使用连续的限制玻尔兹曼机确定吉林南部多元化探异常。O'Brien等^[22]应用RF识别澳大利亚的布罗肯希尔山的断裂山型银铅锌矿床的锌成分。Xiong等^[23]应用深度自编码器探索中国福建地区多元素与铁矿床的关联。Zaremotlagh等^[24]应用DT和ANN识别伊朗中部Choghart矿床的轻稀土元素地球化学分布模式。这些案例研究证明，机器学习模型是识别多元地球化学异常的有用工具。

随着大数据研究的发展和人工智能时代的来临，传统依赖于专家知识的地球化学异常提取方法逐渐无法适应当前飞速发展的社会，如何自动地、不依赖于专家知识提取地球化学异常成为当前需要着重考虑的问题。长期的地质统计学研究表明，地球化学数据有很强的结构性，大多数地球化学异常存在一定的空间分布形态，有格子状、环状、带状等^[25-27]。如果能够通过识别这些特殊的空间分布形态，推断出地球化学异常，将成为地球化学找矿的一种新思路。本文通过分析地球化学数据的元素值属性和空间位置，提出了基于空间邻域约束的聚类算法，旨在从地球化学异常的特殊空间形态角度，自动提取地球化学异常。

1.   研究方法

本文提出的基于空间邻域约束的聚类算法，是在聚类算法的基础上，通过添加邻域约束的条件，形成针对地球化学数据的元素异常提取方法。地球化学数据是一种高维数据，每个采样点含有多个地球化学元素值，且采样稀疏，数据具有稀疏性。根据地球化学数据高维且稀疏的特点，本文的基础算法采用谱聚类算法，并对谱聚类算法的优缺点进行了分析（表 1）。同时，本文选取K-Means算法和基于密度的DBSCAN算法进行对比，对比结果在实验部分予以说明。

表  1  三种聚类算法的优缺点分析

Table  1.  Analysis of advantages and disadvantages of three clustering algorithms

聚类算法	优点	缺点
K-Means	简单易实现，适用性强	需要用户事先指定类簇个数；聚类结果对初始类簇中心的选取较为敏感；容易陷入局部最优
DBSCAN	聚类速度快且能够有效处理噪声点和发现任意形状的空间聚类	当空间聚类的密度不均匀、聚类间距差相差很大时，聚类质量较差；对于高维数据，存在“维数灾难”；参数难设置，且无法指定聚类数量
谱聚类	算法在处理稀疏和高维数据上具有一定的优势	若聚类的维度非常高，由于降维的幅度不够，谱聚类的运行速度会降低

下载: 导出CSV 

| 显示表格

1.1   谱聚类算法

谱聚类是一种基于图论的聚类方法^[28]，是将空间中的数据点连成无向图，根据两点之间的相似度定义两点之间边的权重大小，这样就形成一个带有权重的无向图。谱聚类的过程主要是一个分割图的过程，目的是使分割后的子图内部边权重和尽可能大，而被切割的边的权重和尽可能小，从而保证相似度高的点尽可能在一个子图里，而相似度低的点被分到不同的子图中，最终完成聚类。

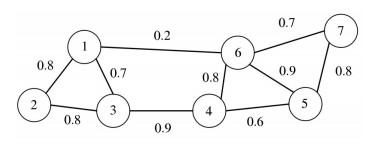
对于一个无向图G，一般用点的集合V和边的集合E来描述，即为G(V, E)。其中V为数据集里面所有的点(v₁, v₂, …，v_n)。对于V中任意的2个点v_i和v_j，若两点之间有边连接，则权重值W_ij > 0，若两点之间没有边连接，则W_ij=0。如图 1所示，对于任意一个点v_i，它的度d_i定义为与其相连的所有边的权重之和，即：

图  1  无向图G

Figure  1.  Undirected graph G

下载: 全尺寸图片 幻灯片

利用每个点度的定义，可以得到一个n×n的度矩阵D，它是一个对角矩阵，只有主对角线有值，对应第i行的第i个点的度数。构建邻接矩阵W的方法最常用的是高斯核函数RBF，此时相似矩阵和邻接矩阵相同，如公式（2）所示：

谱聚类的本质是通过对样本数据的拉普拉斯矩阵的特征向量进行聚类。拉普拉斯矩阵L定义如下：

拉普拉斯矩阵的规范化形式如公式（4）所示：

接下来的工作是分类，谱聚类的分类方式是“切图”。切图的原则：同子图内的点相似度高，不同子图的点相似度低。

谱聚类算法流程：

输入：数据集D=(x₁, x₂, …, x_n)

Step 1：按照公式（2）计算相似矩阵W；

Step 2：将W的对角线值置0，以排除自身的相似度；

Step 3：按照公式（1）计算度矩阵D；

Step 4：按照公式（4）计算归一化拉普拉斯图矩阵L；

Step 5：计算L的特征向量，将前K个特征值最小的向量按列放置成一个矩阵X；

Step 6：对X做行标准化操作，形成特征矩阵F；

Step 7：假设F中每一行有k1维，看作是一个样本，用聚类方法（如kmeans方法）对F矩阵中的特征向量，即样本，进行聚类，聚类数为k2；

输出：簇划分C=(c₁, c₂，…c_k2)。

1.2   邻域约束

尽管谱聚类算法在二维数据上的聚类效果较好，但是不能综合利用空间、元素含量等多重信息。本文对聚类算法进行了改进，提出了一种空间邻域约束的聚类算法。该方法在元素特征聚类的基础上，融入空间特征分析，能有效提取并识别出环状、带状等特殊的空间分布，从而圈定地球化学异常。

地球化学数据是一种复合信息数据，不仅包含多种元素的含量信息，而且包含各个采样点的空间位置信息。在地球化学空间里，某一点与其周围点是同一类的概率比较大。因此，在应用采样点的元素含量值信息聚类后，应用空间邻域约束算法对聚类结果进行修正，将点与点之间的空间位置信息应用到聚类中。

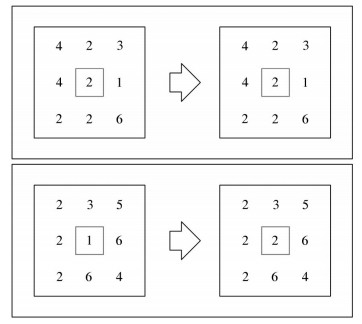
众数滤波是一种数字滤波方法，应用在二维空间里，需要设置一个k×k的窗口，窗口中心位置数据点的值由其周围数据点及其自身的众数值决定（图 2）。这是因为在地质范围内，一个点与其周围点相似的概率比较大，当然也有一些异常点是异于周围点的，但是这样使异常保留的情况降到最低。因此，如果经过此操作，仍然处于异常的，则说明是真的异常。

图  2  空间邻域约束算法演示

Figure  2.  Spatial neighborhood constraint algorithm demonstration

下载: 全尺寸图片 幻灯片

将基于空间邻域约束的聚类算法应用到化探异常的提取中，一般分为以下流程：

输入：地球化学采样点元素含量值及坐标；

Step 1：数据预处理；

Step 2：谱聚类处理；

Step 3：对Step2的聚类结果应用邻域约束算法；

Step 4：可视化Step3的结果；

输出：聚类结果图。

2.   数据和实验

2.1   数据介绍

研究区位于河南省崤山地区，选取高贝沟地区和孤山岭地区的1: 1万地球化学土壤数据。

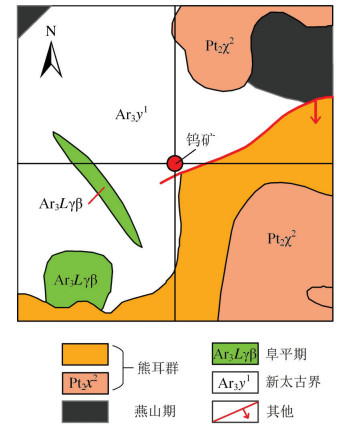
高贝沟地区位于洛宁县长水乡北部，行政区划属洛宁县长水乡，洛宁至长水有省级公路通过，长水至高贝沟有便道相通，交通较便利。通过矿点调查及1:1万地质填图，在区内发现近10条石英脉，呈透镜状出露，沿走向出露2~3m，厚度0.20~1.00m，倾向NE向，倾角一般在30°~60°之间。对该地区进行地球化学数据采样，分析了Cu、Co、Bi、Ni、As、W、Zn、Sb、Mo、Au、Pb、Ag 12种元素。该区地球化学组合异常为W-Ni-Zn-Mo-Au，采样区中部发现钨矿点1处。图 3为高贝沟地区地质图。

图  3  高贝沟地区地质图

Figure  3.  Geological map of Gaobeigou area

下载: 全尺寸图片 幻灯片

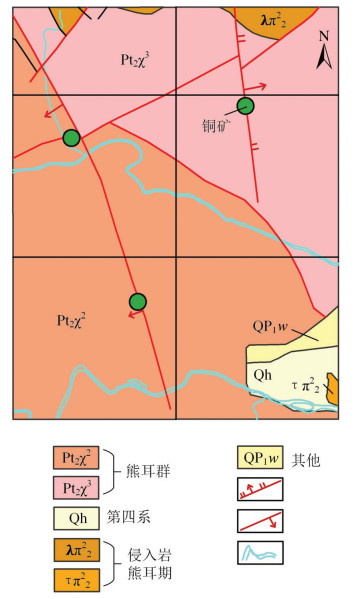
孤山岭矿区位于陕县宫前乡的南部地区。行政区宫前至店子乡公路从调查区西北部通过，其中部有条岔路通往大石涧村的村通公路，交通相对便利。通过矿点调查及1:1万地质填图，在区内发现了多条近SN向及NE向构造带，这些构造带内充填物质多为石英脉及碎裂岩，均有不同程度的黄铜矿化和蓝铜矿化，矿区西北部的几条构造矿化较强，有废弃民采矿硐，构造宽度不超过2m，构造填充物质为石英脉，顶底板为碎裂岩。在矿区东部也有一条较长的构造，控制长度为400m，构造填充物为石英脉，矿化较弱，肉眼仅见褐铁矿化。对该地区进行1:1万数据采样，分析了Cu、Co、Bi、Ni、As、W、Zn、Sb、Mo、Au、Pb、Ag 12种元素。该区主要异常为Cu异常，在采样区内已探明铜矿点3处。图 4为孤山岭地区地质图。

图  4  孤山岭地区地质图

Figure  4.  Geological map of Gushanling area

下载: 全尺寸图片 幻灯片

2.2   实验分析

2.2.1   高贝沟地区实验

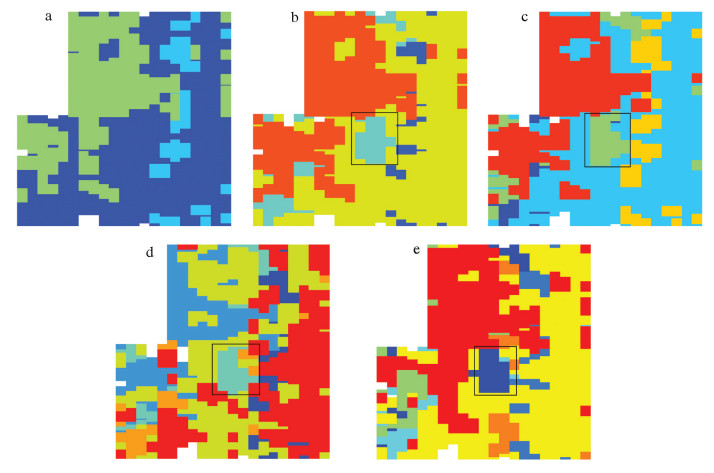
高贝沟地区发现矿点为钨矿，对该地区应用邻域约束聚类算法进行处理，结果如图 5所示。

图  5  邻域约束聚类算法在高贝沟地区提取地球化学异常结果

a—聚3类；b—聚4类；c—聚5类；d—聚6类；e—聚7类

Figure  5.  Results of extracting geochemical anomaly by neighborhood constrained clustering algorithm in Gaobeigou area

下载: 全尺寸图片 幻灯片

图 5为邻域约束聚类算法的处理结果，由于谱聚类算法需要人为指定聚类数，此外，通过改变聚类数而查看聚类结果的变化，也是本文需要探讨的问题之一，因此本文展示了从聚3类到聚7类的结果（图 5）。通过分析，可以得出以下几点结论。

（1）图 5-a中，聚类结果从整体上看大致分为两部分，左上的部分（绿色）和右下的部分（深蓝色），对比图 3可以发现，划分出的这两部分对应新太古界和熊耳群。因此，如果地区不同地层之间差别较大，当聚类数比较少的时候，能够通过聚类结果大致划分出不同地层。

（2）图 5-b~e分别是从4类聚到7类的结果，图中方框标出的位置，存在一个近似于矩形的形状，随着聚类数的增加，该矩形的位置和形状保持相对稳定的状态，是容易引起关注的地方。此外，该矩形在全局范围内属于单独的一个类，且矩形面积相对于全局范围较小，这与本章算法所要寻找的特殊空间形态有一定的相似。事实上，通过图 3的地质图可以看出，矩形区域所在的位置与矿点的位置相隔较近，因此推测该区域很可能是异常区。

2.2.2   孤山岭地区实验

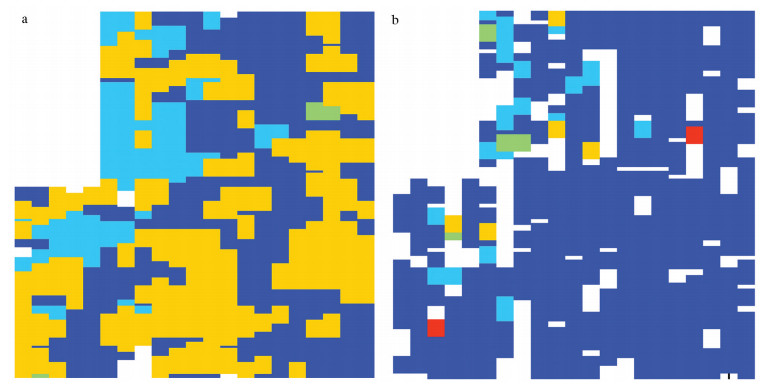
孤山岭地区发现矿点为铜矿，对该地区应用邻域约束聚类算法进行处理，结果如图 6所示。

图  6  邻域约束聚类算法在孤山岭地区提取地球化学异常结果

a—聚2类；b—聚3类；c—聚4类

Figure  6.  Results of extracting geochemical anomaly by neighborhood constrained clustering algorithm in Gushanling area

下载: 全尺寸图片 幻灯片

图 6为邻域约束聚类算法处理的结果。图中a、b、c分别是聚类数为2、3、4的结果。分析图 6，可以得出以下结论。

（1）从整体看，从图 6-a到b再到c，聚类结果变化不大，大致分为2类，一类是面积较大的背景，另一类是区别于背景的部分。地球化学异常的提取，本质是对背景和异常的划分，异常的范围往往少于背景，从面积角度看，异常的面积小于背景的面积。图 6-a、b、c划分的2类，如果假设该结果与地球化学的背景和异常有关，那么图中区别于背景的部分，可以看作是异常类的部分。再对比图 4，图 4中的地层属于同一年代，因此没有像高贝沟地区聚类结果一样对地层有划分。但是图 6中有3个铜矿矿点，矿点的位置包含于图 6-a、b、c划分的异常类中，因此，该方法首先通过聚类结果划分为背景和异常区，从而锁定异常可能存在的范围。

（2）锁定了异常可能存在的范围后，需寻找是否存在特殊形状。图 6-a、b、c中圆圈标识的位置，形成了环状的空间分布，对比图 4，发现环状形态所在的位置，有1个铜矿矿点。该地区共有3个矿点，由于环状形态只出现了一次，因此，并未完全实现所有矿点的识别，但是出现特殊形态的地方，能够指示矿点的存在。在这一点上，该地区的聚类结果与高贝沟地区的结果具有一致性。

（3）该地区还有一处较特殊的地方，就是出现在区域内的2条河流，即图 6-a、b、c对应的白色区域，该位置出现白色并不是单独聚成的一类，而是因为在河流的位置，无法进行土壤采样，因此，河流的地区没有数据。从图 6可以看出，异常类集中分布在河流附近。因此，该地区的河流区域与异常存在关联关系，在实际勘探中，应该引起重视。

2.2.3   不同聚类算法的对比实验

分别以K-means聚类、DBSCAN聚类和谱聚类为基础算法，结合邻域约束对高贝沟地区的数据进行聚类处理，结果如图 7所示。由图 7可以看出，Kmeans算法分出的类别，较均匀地散落在全局；DBSCAN分出的类别区分度不高，基本是一个大类加一些零散的点，这2种算法均不如谱聚类的效果明显。因此，从数据特点、算法适用性及实验结果3个方面均证明本文提出的邻域约束谱聚类算法在处理地球化学数据上优于其他聚类算法。

图  7  两种聚类算法与邻域约束结合处理高贝沟地区的数据结果

Figure  7.  Results of three clustering algorithms combined with neighborhood constraints in processing data in Gaobeigou area

a—K-means; b—DBSCAN

下载: 全尺寸图片 幻灯片

3.   结论

（1）邻域约束聚类算法需要人为指定聚类数，一般以该地区地质图所含主要岩石的数目为参考，如高贝沟地区为5类，孤山岭地区为2类，在此基础上增加或减少类的数量，从而从多角度观察聚类的结果。

（2）聚类结果因地区而异，一般出现特殊形状，且在多幅聚类图中特殊形状保持稳定的情况下，该特殊形状为地球化学异常的可能性较大，且与矿点具有关联性。特殊形状一般面积不大，可能是环状、半环、矩形等。

（3）如果地区具有不同年代的地层，则通过较少的聚类数聚类，结果能够对地层有所划分。如果地区属于同一年代的地层，则聚类结果大致能够对背景和异常区有所划分，但是该异常区范围较大，虽然能够涵盖地区内大部分地球化学异常，还是需要进一步提取更精确的异常区域。

（4）邻域约束聚类算法能够不依赖于专家经验，自动地将地球化学异常以聚类结果中的特殊形态的形式呈现出来，具有普适性和高效率，能够适应大数据环境下大规模数据的处理模式。但是该方法也存在异常提取的粒度不够精细的问题，需要进一步缩小异常提取的范围，做到更加精确地圈定找矿靶区。